Another classic problem solving question - Konigsberg Bridge! To put it simply: People tried to find a way to walk all seven bridges without crossing a bridge twice, but no one could find a way to do it… until Euler came to explain why! And his analysis on this problem was the first of Graph Theory - of vertices, edges and faces.
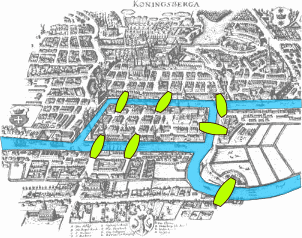
And Euler concluded that it was not possible to cross the bridges only once. Euler general law states: A path traversing the network of crossing every segment once is possible if the network is connected and has at most 2 vertices with odd valence (number of edge ends at the vertex). some other links on this interesting problem: